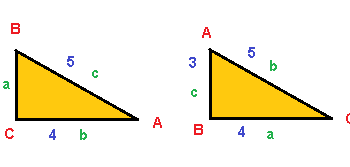
Teorema del seno
Uso del teorema del seno El teorema del seno en CNC se utiliza en ocasiones donde es necesario saber una longitud determinada en un triángulo "no rectángulo". Para esas situaciones existe este teorema. Por ejemplo, la longitud de uno de sus lados, un ángulo determinado, etc... Cuando nos encontramos con esto, tenemos que acudir a los teoremas del seno y del coseno. Breve definición del teorema del seno En concreto, en este teorema, el del seno, nos dice que: La relación existente entre un lado y el seno del ángulo opuesto a ese lado, es siempre igual para todos (lados y ángulos restantes). La siguiente ilustración aclarará todo tipo de dudas. Como se comenta arriba, la relación existente entre el lado A y el seno del ángulo alfa, es la misma que la relación existente entre el lado B y el seno del ángulo beta. Por lo tanto: Comprobación en los cálculos de cualquier triángulo La ecuación de Mollweide Para realizar la comprobación de este tipo de cálculos puedes usar la ecuación de Mollweide. Esta fórmula la puedes utilizar para cualquier tipo de triángulos, independientemente si son rectángulos o no. Puedes ver su uso en esta entrada. ;-) Verás que te será de gran ayuda el poder comprobar numéricamente un cálculo trigonométrico sin necesidad de tener que dibujar la figura en AutoCAD o algún otro…